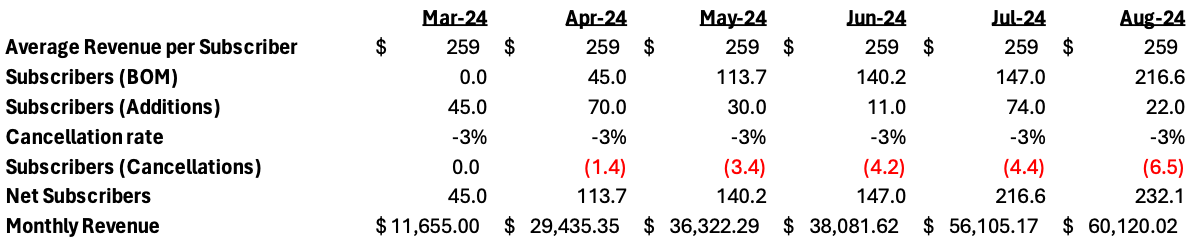Recurring Revenue Modeling Can Be Tricky, Using Cancellation Curves Can Improve Precision And Results

 In a recent post on recurring revenue financial modeling, I covered some of the main drivers that play a role in the construction of financial forecasts for SaaS and related business models. One of the most important aspects of such financial forecasts is the build out of contracted revenues. In general contracted revenues can be quite predictable, which makes the recurring revenue model so attractive to investors.

The Basics

In a basic format, the recurring revenue forecasting for a good financial model will have the following components to calculate the monthly revenue:

1. Average revenue per subscriber

2. Number of subscribers, beginning of the month (past bookings)

3. Number of subscribers added in the month (new bookings)

4. Composite cancellation rate (the expected % of existing subscribers who will cancel in the month)

5. Number of subscribers lost in the month (2*4, cancellations or churn)

6. Net number of subscribers (2+3-5)

7. Revenue for the month (1*6)

The image below shows a recurring revenue forecast based on the above calculations. It is necessary to understand that in this kind of model, the limited variations in average revenue and cancellation rates lend themselves to a composite view of the revenue build. If these underlying simplifications are reliable, the above methodology works just fine.

Pro-tip: Unless you have some strong need, I allow subscribers to be calculated in fractions and avoid any rounding functions for subscriber counts. I find partial clients (even though there is no such thing) makes models easier to manage because rounding functions sometimes have unintended consequences and also require maintenance and awareness of their use when other people are using your model.

More complex subscriber calculations

But, what if average revenue per subscriber changes for each new cohort of subscribers and the cancellations vary based on the age of the client. In this case, the value of the existing contracted backlog and the forecast of future contracted backlog becomes much more complex. You can stick to the above methodology, but with cancellations being age dependent, you could be in for hidden surprises and also leave your operations teams with a less refined set of objectives when they are trying to reduce cancellations.

One way to resolve this complexity is to look at a cohort-based backlog, which accounts for the average revenue variation by specifically assigning a revenue amount to a cohort and also assigning a cancellation percentage to each cohort based on its age. In this kind of model, each cohort is assigned a date of birth (sometimes called a vintage) so that it can be tracked uniquely throughout time.

The image below shows what the cancellations would look like in a cohort-based format. (I am intentionally ignoring revenue variations, but this would use a similar methodology to accommodate that variation.) Notice how each month of the model needs to have a cancellation percentage for each cohort.

Compared to the basic format at the beginning of this post, the cohort-based format has turned into a matrix instead of being a single vector (line) of the spreadsheet. In fact, to do this precisely, each line of the basic format should become a matrix. Then instead of multiplying lines in Excel, you multiply across matrices to get to revenue.

Using rough math, the composite cancellation rate in the matrix is about 3% over the March to August time frame. However, you can see that the Aug-24 ending revenues in the cohort-based format ($59,420) are slightly lower than the basic format ($60,120). Now you might think that the $700 (1.1%) is not a big deal, but over time and with increased volume this variance will grow and lead to weaker forecasting. While I would love to use a simpler model for expediency, it does not stand to scrutiny when you want to have reliable forecasting of revenues.

Summary

Tracking recurring revenues is tricky and precision comes with model complexity. I find that the complexity is worth it because it instills confidence in your audiences over time and also provides the operations teams with very specific data about handling the execution on their end. For example, in the cohort-based format above, but not shown here, I would easily provide a forecasted cancellation count by age of the subscriber, which enables the operations team to manage their targets very specifically during the subscriber lifecycle journey.

One final note: this post only deals with the build up of subscribers in the future. If you have existing subscribers, you can use the same methodology but you should not mix the existing cohorts with the projected ones. The matrices go in different directions and they are hard to combine. Manage them in separate files if needed. I hope to do a post on that in the future.

FAQs for Recurring Revenue Modeling using Cohorts:

1. Why is cohort-based forecasting important in recurring revenue modeling?Cohort-based forecasting is crucial in recurring revenue modeling because it allows for a more accurate representation of revenue streams by considering variations in average revenue per subscriber and cancellation rates based on the age of the client cohorts. This approach provides a more granular and precise understanding of revenue projections, enabling better decision-making and operational strategies.

2. How does cohort-based forecasting differ from basic recurring revenue modeling?In basic recurring revenue modeling, calculations are simplified by using composite averages for revenue per subscriber and cancellation rates. In contrast, cohort-based forecasting assigns specific revenue amounts and cancellation percentages to each cohort based on their unique characteristics, such as date of birth or vintage. This results in a more detailed and nuanced analysis of revenue trends over time.

3. What are the benefits of using cohort-based forecasting in revenue modeling?Utilizing cohort-based forecasting in revenue modeling offers several advantages, including enhanced accuracy in predicting revenue fluctuations, better insights into subscriber behavior over time, and the ability to provide operations teams with specific data to optimize customer retention strategies. While this approach may introduce complexity, the precision it brings to forecasting can lead to more reliable financial projections and improved operational efficiency.

Using a Survival Model for Credit Risk Scoring and Loan Pricing Instead of XGBoost

In the consumer lending space, fintech companies have innovated many aspects of the consumer experience. One of the biggest innovations has been the real-time approval of consumers for installment loans with borrowed cash hitting consumer bank accounts in an expedited and highly satisfying way. For those of you not in the business, the loan origination system, as we often call it, provides all of the capabilities to take a credit shopper and turn them into a borrower. To drive this positive consumer experience, fintech lenders rely heavily on real-time credit-scoring processes built into the loan origination system.

Many fintech lenders have advanced innovations using machine learning and data science to develop algorithms that provide a consumer risk score (probability of default) and loan price (interest rate and APR) to the consumer. These algorithms generally ingest consumer credit and financial data to discern the risk of a consumer and provide an appropriately priced installment loan, if possible, given the risk profile.

At the heart of many of these algorithms lies tree-based classification algorithms such as the XGBoost machine learning model, which seeks to classify consumers into risk categories based on their credit and financial profiles. Loan pricing is subsequently determined to generate a profitable loan. Sometimes, for simplicity, loan prices might be determined statically for each risk bucket; for example, all consumers rated a B+ receive and interest rate of 17.99%. Other more sophisticated pricing approaches might provide dynamic pricing.

We used this approach in the past, but in a new effort, we decided to calculate risk and pricing in a manner that aligns more closely to typical fixed income cash flows. In other words, if a consumer installment loan is a series of cash flows, why not calculate the probability of default for each payment and then do a risk adjusted discounted cash flow valuation of the loan that generates a specified profit regardless of risk? In this manner, the loan pricing accounts for the risk of each cash flow and all loans could be targeted to achieve our profit target with interest rates increasing as risk increases.

This approach evolved from research that one of our data scientists did when examining credit risk pricing models and discovered previous academic research using a survival regression algorithm to predict the payment-by-payment probabilities of default for the duration of the loan. A survival regression model is a technique that models the time until an “event” occurs. This family of models is often used in health-care related analysis, where “survival” means exactly that – did the subject survive to the next period. In our case, survival means “no default on payment” in this period, or that the loan value survives to the next payment.

By taking into account credit and financial factors of the individual influencing a potential event of default and a probability of the event of default occurring at payment of the loan, a projected series of default probabilities is generated for the entire loan duration. This series is called the “hazard function curve”. The same risk profile can also be represented in another curve called “survival curve” where each point in the curve denotes the likelihood that a borrower will not default up to the specific point in time.

Here, for three applicants, are the hazard function curves (showing the probability of default at each loan payment) and the survival function curves (showing the probability of no-default up to each loan payment) for a 36-month installment loan.

The two figures display the same three applicants: A, B and C, in two ways, using the cumulative hazard function and the survival function. The higher the forecasted cumulative hazard curve throughout the months, the lower the ending survival probability of the applicant.

The Cox Proportional Hazards algorithm is the specific survival regression method we improved upon to forecast this series of default probabilities throughout the loan term, as shown in the Hazard Function Curve above. Each point on this hazard curve represents the likelihood that the borrower will default on the loan in a specific month, given no default has occurred up to that point. Similar to other supervised machine learning algorithms, we trained the Cox Proportional Hazards model on a dataset comprising historical loan originations, which includes the borrower's financial attributes, loan default status, and time-to-default labels. Once trained, the model evaluates in real-time the default curve (Hazard Function Curve) for a prospective borrower based on their financial attributes, utilizing the predictive power learned from the model features.

The remaining loan origination process requires only fundamental financial analysis to price the loan based on the modeled risks. By applying this resulting default curve to a series of loan payments, we construct a risk weighted cash flow series for the consumer loan. With that series of expected value cash flows, we apply interest rate expenses using a forward curve: In our case, we use the SOFR 1-month forward curve plus our cost of capital spread. We leave a target variable to flex for our interest margin, which iteratively solves (we use an optimization function) to reach the targeted Net Present Value of the loan, which also factors in all origination costs, servicing costs and capital lent to the borrower.

Reference: https://t.co/dkRCobwfts